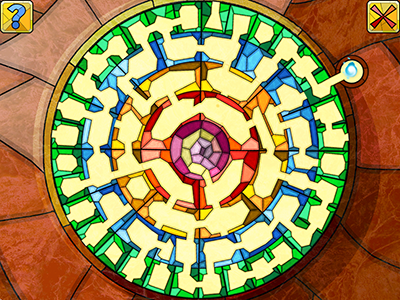
Chi ha già avuto modo di provare il nostro gioco, Little Briar Rose, si sarà trovato di fronte a un ostacolo in particolare: Il labirinto del fungo.
Cercando la soluzione da soli o con l’aiuto degli indizi, in molti sarete riusciti a superare la prova.
Altri, invece, avranno scoperto dei percorsi nuovi a noi sconosciuti. Questo è quel che si dice “un errore di calcolo”.
Sapevamo della possibilità che, casualmente, si sarebbero potute creare delle strade aggiuntive durante lo sviluppo della grafica. Eravamo comunque fiduciosi di poter sistemare il tutto nella fase di test.
Se il nostro modesto team non poteva prevedere a priori le strade multiple, il problema si sarebbe risolto quando molte più persone avrebbero provato la versione Beta del gioco.
Risolte molte delle combinazioni erronee, eravamo certi di aver battuto tutte le strade. Ma ci sbagliavamo.
Dopo solo un giorno dal rilascio ufficiale, alcuni utenti armati di screenshot ci segnalavano già due percorsi inattesi, riportando la nostra attenzione sul problema.
L’enigma è in sé abbastanza semplice. C’è un labirinto formato da un certo numero di cerchi concentrici. I cerchi possono essere ruotati, e su ogni cerchio sono presenti varie stanze adiacenti, con strade che permettono di muoversi da una stanza all’altra. L’obiettivo del gioco è quello di creare un percorso che permetta allo spiritello di raggiungere il centro del labirinto.
Come abbiamo pensato e creato l’enigma?
Inizialmente abbiamo provato un approccio procedurale, abbandonato in fretta per ottimizzare il poco tempo a disposizione.
In seguito, abbiamo optato per un approccio più retrò, ma sicuramente più divertente:
Ci siamo muniti di forbici, cartoncino e pennarelli, e abbiamo costruito manualmente i vari enigmi. Partendo dalla soluzione iniziale abbiamo scombinato e l’enigma e generato altri percorsi, volutamente ciechi.
Con il primo enigma è stato semplice: è bastata qualche prova per ottenere un enigma ben calibrato e privo di errori.
Man mano che gli enigmi si facevano più complessi, anche individuarne le soluzioni multiple si faceva più impegnativo.
Come abbiamo risolto?
La questione è sempre: qual è la soluzione più semplice al problema, che mi permetta di risolverlo nel minor tempo possibile, senza sacrificare l’accuratezza?
La risposta è: provare tutte le alternative.
Facciamo un rapido conto. Nell’enigma più complesso, ogni cerchio può assumere diverse posizioni. In dettaglio:
- Primo cerchio: 8 stati
- Secondo cerchio: 16 stati
- Terzo cerchio: 32 stati
- Quarto e ultimo: 64 stati
Per un totale di 8*16*32*64 = 262.144 combinazioni. Niente male.
Se vi state chiedendo come fa il giocatore a risolvere un enigma con tutte queste combinazioni, la risposta è semplice: Gran parte dei percorsi sono evidentemente ciechi e non portano a nulla, eliminando del tutto la necessità di esplorarli per l’occhio umano.
La domanda resta: come verificare quali di questi stati portano a una soluzione valida per il gioco, pur non essendo concepita?
Ho valutato varie opzioni, tra cui algoritmi di pathfinding. Tuttavia, avrei perso troppo tempo a costruire il grafo delle stanze e i vari percorsi, necessario all’algoritmo per funzionare.
Infine ho optato per un approccio visivo, utilizzando lo strumento più semplice che ogni programma di grafica mette a disposizione: il “riempimento” o “secchiello”. L’algoritmo usato per questa operazione è detto Flood Fill.
Come funziona: Ricevendo in input un certo pixel di un’immagine e un colore destinazione, vengono individuati tutti i pixel adiacenti aventi un colore simile al pixel selezionato. I pixel individuati vengono dunque colorati col colore destinazione. La procedura viene ripetuta con i pixel adiacenti finché tutta l’area con lo stesso colore viene ricolorata.
Ecco un’immagine esplicativa da Wikipedia:

Ed ecco come ho dunque usato il Flood Fill per identificare i percorsi validi:
- Posiziono il mini game in un certo stato, ruotando i cerchi coerentemente
- Faccio uno screenshot scalato del gioco
- Applico l’algoritmo Flood Fill, selezionando un pixel nei pressi del punto di partenza
- Controllo se la destinazione viene colorata del colore scelto.
- Ripeto con lo stato successivo
Trovate qui l’implementazione del Flood Fill in C# utilizzata:
Un paio di note implementative:
Ho provato anche un approccio ricorsivo, che risulta più semplice da implementare. Purtroppo risultava estremamente lento e ben presto falliva con uno “Stack Overflow”.
Inoltre da notare come ho pre-allocato la dimensione dello stack a una sicuramente maggiore di quella che verrà effettivamente usata dall’algoritmo (nello specifico, il totale di pixel dell’immagine). Questo perché l’allocazione dinamica è una procedura lenta. Inoltre questo mi ha permesso di individuare bug ed errori di implementazione, che portavano l’algoritmo a ciclare indefinitamente.
Quest’ultimo dettaglio ha ridotto i tempi di esecuzione del FloodFill da secondi a millesimi di secondo. Il che è molto importante, visto che le soluzioni da esplorare erano più di 200mila.
Ecco un esempio di output:
Ed ecco l’algoritmo che gira!
Grazie a questo metodo, siamo riusciti a individuare più di 18 percorsi non previsti dal mini gioco, che la nostra artista Fabiola ha provveduto a rimuovere. Il tutto in meno di un pomeriggio, implementazione inclusa.
Talvolta la soluzione più semplice è quella vincente!
Alla prossima!